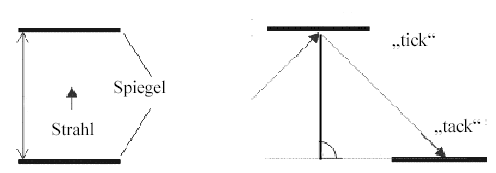
Mit dem Messen ist das manchmal eigenartig. Eine der berühmtesten Messungen in der Geschichte der Physik war „unscharf“. Heisenberg stellte fest, dass man die Position und die Geschwindigkeit eines Teilchens, eines Elektrons nämlich, nicht gleichzeitig genau bestimmen kann. Für seine Messungen hatte sich angeboten, die Teilchen mit Licht zu bestrahlen. Einige der Lichtstrahlen würden durch die Teilchen gestreut, so dass man ihre Position erkennen konnte. Doch Licht bewegt sich zyklisch, so dass die Genauigkeit, mit der sich die Position eines Teilchens bestimmen lässt, durch die Frequenz des jeweiligen Lichts begrenzt ist. Um die Messgenauigkeit zu erhöhen, muss man Licht mit hoher Frequenz einsetzen. Je höher die Frequenz der Strahlung ist, desto höher ist jedoch auch ihr Energiegehalt. Die Energie, mit der das Licht auf das Teilchen trifft, beeinflusst wiederum die Energie, das heißt die Bewegung des Teilchens selbst. Sie wird verändert. Wollte man also die Geschwindigkeit des Teilchens genau messen, dann brauchte man dazu eine möglichst energiearme Strahlung, das heißt Licht mit niedriger Frequenz.
Da haben wir es – ein klassisches Dilemma: Für die genaue Messung der Position braucht man energiereiche Strahlung und für die Messung der Geschwindigkeit energiearme. Wenn man beides gleichzeitig messen will, steht man vor einem unlösbaren Problem. Kann man den Feind nicht besiegen, muss man ihn zum Verbündeten machen. Heisenberg verpackte sein Dilemma in mathematische Konstrukte, um mit ihnen das Verhältnis beider Unschärfen zu bestimmen. Mit seiner Unschärferelation ging er in die Geschichte der Physik ein. Es blieb jedoch die Frage, ob es sich bei der Unschärfe um die Begrenztheit der Messmöglichkeiten handelt oder ob die Natur selbst „unscharf“ sei. Die Tatsache, dass sich die Position und die Geschwindigkeit eines Teilchens relativ genau bestimmen lassen, nur eben nicht gleichzeitig für das selbe Teilchen, legt die Vermutung nahe, dass das Dilemma der Unschärfe aus der Begrenztheit der Messmöglichkeiten resultiert. Jedenfalls war Einstein dieser Meinung, hier allerdings im Gegensatz zu vielen seiner Kollegen.
Tatsächlich haben wir es mit einem grundsätzlichen Problem aller Messungen in Grenzbereichen zu tun. Für eine Messung brauchen wir neben dem Maßstab immer auch ein Messverfahren beziehungsweise ein Messinstrument. Dieses Instrument muss in seinen Eigenschaften etwas weiter gehen, eine größere Bandbreite abdecken, als das zu Messende selbst. Zum Beispiel muss ein Thermometer, um Temperaturen von minus 40 Grad Celsius messen zu können, selbst in der Lage sein, in diesem Temperaturbereich vorherbestimmbar zu reagieren. Schlicht gesagt, muss seine Skala mindestens minus 41 Grad zulassen. Würde es bei minus 40 Grad Celsius enden, wüssten wir nicht, ob beim Erreichen des Endpunktes der Skala dieser Wert das Messergebnis ist oder ob nicht ein anderes Ergebnis angezeigt würde, wenn es denn möglich wäre. An dieser Stelle drängt sich die Frage auf, wie man eigentlich Temperaturen nahe dem absoluten Nullpunkt misst. Eine direkte Messung ist nicht möglich, da das Messinstrument in der Lage sein müsste, den absoluten Nullpunkt anzuzeigen, um ein zweifelsfreies Ergebnis zu erzielen. Da es keinem Stoff der Natur möglich ist, eine Temperatur von 0 Grad Kelvin anzunehmen, kann es kein Messinstrument geben, das diese Forderung erfüllt. Für Messungen im Bereich des absoluten Nullpunkts muss man daher physikalische Analogien heranziehen und Berechnungen durchführen. Dabei muss man eventuelle zusätzliche Fehlerquellen in Kauf nehmen.
Wie misst man eigentlich die Lichtgeschwindigkeit? Für eine direkte Messung würde man wiederum ein Messinstrument benötigen, dass das Licht überholen kann. Es würde mit dem Licht starten und vor dem Licht an einem Messpunkt eintreffen. Dabei legte es exakt die gleiche Strecke wie das Licht bei durchgängig identischen äußeren Bedingungen zurück. Da die Geschwindigkeit des Messinstruments dokumentierbar ist, könnte die Geschwindigkeit des Lichts im Vergleich zum Messinstrument mit hoher Genauigkeit ermittelt werden. Ein solches Instrument steht jedoch nicht zur Verfügung, da die Lichtgeschwindigkeit nicht übertroffen werden kann. Zur Bestimmung der Lichtgeschwindigkeit bleiben auch hier nur Analogien und Berechnungen mit den ihnen immanenten möglichen Fehlern. Das Heisenbergsche Problem ist, so gesehen, nicht grundlegend von den Problemen des Messens im Bereich des absoluten Nullpunkts oder der Bestimmung der Lichtgeschwindigkeit verschieden. Eine direkte Messung ist in Grenzbereichen nicht möglich und jede indirekte Messung ist mit Ungenauigkeiten, mit einer „Unschärfe“ behaftet. Das Verdienst Heisenbergs besteht vor allem darin, diese Unschärfe für sein Gebiet quantifiziert zu haben.
Wenn ich mir das so richtig überlege, dann sind nicht nur die Messungen in Grenzbereichen mit Fehlern behaftet, sondern alle Messungen. Fehler können aus der Ungenauigkeit des Messverfahrens oder aus Abweichungen im verwendeten Maßstab resultieren. Zudem sind die Umstände der Messungen nie absolut identisch, was die Vergleichbarkeit der Ergebnisse beeinträchtigt. Außerdem kann man nicht verhindern, dass sich diese Umstände auch während des Messvorganges verändern. Selbst wenn die Abweichungen minnimal sein sollten, so sind sie doch Fehlerquellen. Man muss sich also bei jeder Messung darüber im Klaren sein, dass sie Ungenauigkeiten beinhaltet. Im Alltag ist das meist nicht von Belang. Wenn ich einen Zollstock zur Hand nehme, werde ich kein Messergebnis mit einer Genauigkeit von 0,01 Millimeter erwarten. Deshalb ist es in diesem Fall auch unwichtig, dass bei Zimmertemperatur, also nicht bei 0°C, wie für den Urmeter vorgesehen, gemessen wurde. Womöglich war der Zollstock nicht einmal völlig gerade aufgeklappt. Trotz dieser und anderer Fehler genügt die erreichte Genauigkeit, um den Tisch zu vermessen, damit eine passende Decke ausgewählt werden kann.
Bei anderen Messungen, die eine deutlich höhere Genauigkeit verlangen, ist es erforderlich, möglichst viele Fehlerquellen auszuschließen oder deren Einfluss zu minimieren. Gleichzeitig sollten alle erkannten Fehlerquellen dokumentiert werden. Wenn man die mögliche Größe der Fehler quantifizieren kann, dann ist es durchaus sinnvoll, den Messergebnissen eine Wahrscheinlichkeit in Bezug auf ihre Genauigkeit zuzuordnen. Diese Wahrscheinlichkeit, das heißt den Grad der Genauigkeit, kann man unter Umständen steigern und schrittweise einer absoluten Genauigkeit annähern, ohne dass diese jemals erreicht würde. Die Dezimalzahlen spiegeln diesen Zusammenhang eindrucksvoll wider. Man kann ihnen unendlich viele Stellen nach dem Komma anfügen und damit jede gewünschte Genauigkeit ausdrücken. Mit der Unendlichkeit der anfügbaren Stellen machen sie gleichzeitig deutlich, dass eine absolute Genauigkeit nicht erreichbar ist.
Nehmen wir ein anderes Beispiel. Die Zahl Pi hat man auf unvorstellbar viele Stellen nach dem Komma berechnet, ohne dass die Rechenoperation zu einem Ende gekommen wäre. Das heißt, die Genauigkeit der Berechnung von Pi ließe sich weiter steigern, ohne die Zahl abschließend bestimmen zu können. Mit anderen Worten, niemand kennt die genaue Größe von Pi. Trotzdem ist unstrittig, dass diese Zahl einen tatsächlichen Zusammenhang widerspiegelt, denn dieser ist durch unzählige praktische Anwendungen belegt. Mathematiker haben ohnehin kein Problem damit. Für sie ist das Umgehen mit absoluten und relativen Bestimmtheiten nichts Besonderes. Sie haben zum Beispiel Methoden entwickelt, mit denen sich Grenzwerte in der Unendlichkeit, also in einer nicht bezifferbaren Dimension, ermitteln lassen. Trotzdem wird die praktische Relevanz dieser Berechnungen von niemanden in Frage gestellt. Der Fakt, dass man mit den zur Verfügung stehenden Methoden eine Größe nicht mit letzter Genauigkeit bestimmen kann, ist also kein hinreichender Grund dafür, deren Existenz zu verneinen.
Im Zusammenhang mit der Unschärferelation ist noch ein weiterer Aspekt von Bedeutung. Heisenberg hatte mit Elektronen gearbeitet, die als Teilchen galten. Man ordnete ihnen eine Masse zu. Max Planck hatte wiederum dargelegt, dass Licht und andere energetische Strahlung nicht in beliebig kleinen Portionen abgegeben wird. Es gibt einen Grenzwert, ein jeweils kleinstes Quantum, mit der sich Energie ausbreitet. Die Größe dieses kleinsten Quantums ist proportional zur Frequenz der jeweiligen Strahlung. Außerdem stellte man fest, dass die Quanten ganz verblüffende Eigenschaften haben mussten. Sie schienen Wanderer zwischen einer Welt der Teilchen und einer Welt der elektromagnetischen Wellen zu sein, waren sie doch zu jedem beliebigen Moment scheinbar in beiden Welten zu Hause. Das galt auch für die Elektronen. Schon deshalb mussten sie sich, so die These, einer genauen Bestimmung entziehen. Auf der einen Seite war da also ein Messproblem. Was man auch anstellte, man konnte ein Elektron nicht gleichzeitig genau in Ort und Zeit bestimmen. Auf der anderen Seite gab es diesen nicht recht erklärlichen Dualismus, der bewirkte, dass das Elektron scheinbar gleichzeitig als Welle und als Teilchen agierte. Die Schnittmenge beider Probleme führte zur Schlussfolgerung, dass das Elektron nicht bestimmbar sei, weil es selbst in Ort und Zeit unbestimmt ist. Dieses unbestimmte Teilchen würde erst durch die Messung einzelner seiner Aspekte eine Bestimmung, eine bestimmte Existenz erhalten.
Das ursprüngliche Messproblem wird auf diese Weise zum Naturphänomen. Mehr noch, der Messende avanciert zum Schöpfer, denn nur durch seine Messung erhält das Teilchen seine Bestimmtheit. Mit diesem Ansatz werden allerdings weder die Grenzen der Messgenauigkeit noch das Wesen der energetischen Strahlung wirklich erklärt. Die offenen Fragen werden lediglich ins Reich des Unbestimmbaren verschoben, was Einstein zu der Bemerkung provozierte: „Gott würfelt nicht“, mithin die Welt muss eindeutig sein.
Bild: fotocommunity.de
zuletzt geändert: 30.05.2019