Das Verständnis des Messens spielt auch bei einer der berühmtesten Theorien der Physik eine fundamentale Rolle, bei Einsteins Spezieller Relativitätstheorie.
In der zweiten Hälfte des 19.Jahrhunderts hatte James Clerk Maxwell dargelegt, dass Licht eine elektromagnetische Welle sein muss, die sich ebenso wie andere elektromagnetische Wellen mit einer endlichen konstanten Geschwindigkeit, der Lichtgeschwindigkeit, ausbreitet. Lange Zeit war man zudem der Meinung gewesen, dass der Weltraum von einem Stoff ausgefüllt sei, den man Äther nannte. Der Äther würde das Medium sein, in dem sich die elektromagnetischen Wellen ausbreiteten, ähnlich den Schallwellen in der Luft. Außerdem sollten sich deren Bestandteile zueinander in Ruhe befinden, so dass der Äther auch den Bezug für die Bestimmung der absoluten Geschwindigkeit des Lichts bilden würde.
Einstein war nun zu der Überzeugung gelangt, dass es einen Äther nicht gibt. Alle theoretischen Ansätze, die einen Äther postulierten, hatten sich als nicht haltbar erwiesen. Wenn es keinen Äther gab, dann konnte man auch keine absolute Geschwindigkeit des Lichts messen, da die Messung einer absoluten Bewegung nur in Relation zu ruhenden Objekten möglich ist. Wenn man eine absolute Bewegung des Lichts nicht messen kann, dann konnte sie, nach seiner Überzeugung, auch nicht existieren. Folglich musste die Maxwellsche Forderung zum Licht, sich mit endlicher und konstanter Geschwindigkeit auszubreiten, für alle messbaren, mithin alle relativen Bewegungen des Lichts gelten. Das heißt, es kann keine relative Geschwindigkeit geben, die höher als die Lichtgeschwindigkeit ist.
Vor diesem Hintergrund ist die Frage zu beantworten, was geschieht, wenn sich ein Beobachter in einer relativen Bewegung zum Licht befindet? Für unsere Überlegungen betrachten wir einen Lichtstrahl, der sich fokussiert in eine Richtung ausbreitet. Nehmen wir an, ein Beobachter könnte diesen Lichtstrahl parallel und mit Lichtgeschwindigkeit begleiten. In Analogie zu der von uns betrachteten Autojagd würde das bedeuten, dass sich der Lichtstrahl nicht vom Beobachter entfernt. Das heißt, in dem vom Beobachter mit dem Lichtstrahl gebildeten Bezugssystem wäre die relative Geschwindigkeit der beiden Protagonisten zueinander Null. Dies widerspräche jedoch der Relativitätstheorie. Die ihr zugrunde liegende Prämisse besagt, dass die relative Lichtgeschwindigkeit, das heißt, die im Verhältnis zu jedem beliebigen Objekt gemessene Geschwindigkeit des Lichts immer und überall gleich sei. Mit anderen Worten, „egal, wie schnell sie hinter einem Lichtstrahl herjagen, er entzieht sich ihnen mit Lichtgeschwindigkeit“(1). Das klingt paradox, ist es wohl auch. Noch deutlicher wird das Paradoxe dieses Ansatzes, wenn wir einen zweiten Beobachter, der an Ort und Stelle verharrt, zu unserer Betrachtung hinzunehmen. Der erste Beobachter, der dem Lichtstrahl hinterherjagt, entfernt sich mit Lichtgeschwindigkeit vom verharrenden Beobachter. Der Lichtstrahl – so die spezielle Relativitätstheorie – entfernt sich ebenfalls mit Lichtgeschwindigkeit von seinem Verfolger. Das hieße jedoch, der Lichtstrahl müsste sich nun mit doppelter Lichtgeschwindigkeit vom verharrenden Beobachter entfernen, jedenfalls nach gängiger Logik. Doppelte Lichtgeschwindigkeit ist jedoch ausgeschlossen. Und nun?
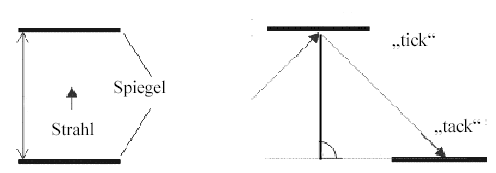
Wechseln wir zu einem anderen Gedankenexperiment, das im Zusammenhang mit der speziellen Relativitätstheorie häufig angeführt wird. In diesem Gedankenexperiment bedient man sich zur Messung der Zeit einer Lichtuhr. Durch deren einfache Konstruktion sind äußere und innere Einflussfaktoren weitgehend ausgeschaltet (2). Eine Lichtuhr besteht aus zwei parallelen Spiegeln, zwischen denen ein Photon hin- und herläuft. Jedes Anschlagen des Photons an einen Spiegel sei eine Zeiteinheit. Es wird nun die Frage gestellt, ob eine Bewegung der Uhr Einfluss auf die Zeitmessung hat. Würden eine stationäre und eine bewegte, das heißt gleitende Lichtuhr das gleiche Resultat der Zeitmessung erbringen?
stationäre Lichtuhr gleitende Lichtuhr
Man betrachtet den Weg, den das Photon aus Sicht eines außen stehenden Beobachters zurücklegt. In der stationären Uhr ist es ein gerader vertikaler Weg A zwischen den beiden Spiegeln. In der bewegten Uhr kommt aus der Sicht des Beobachters zu der vertikalen Bewegung des Photons die horizontale Bewegung der Uhr mit einem Betrag B hinzu. Aus der Summe beider Bewegungen resultiert eine Diagonale, die den Weg des Photons aus der Sicht des außen stehenden Beobachters beschreibt. Die Diagonale C, die das Photon von einer Berührung des Spiegels bis zur nächsten Berührung zurücklegen muss, ist länger als der vertikale Weg A. Da die Geschwindigkeit des Photons gleich bleibt, sein Weg aber länger wird, muss sich ein anderer Faktor verändern. Als solcher Faktor bliebe nur die Zeit. Das heißt, das Zeitintervall, in dem das Photon in der gleitenden Lichtuhr den Spiegel berührt, müsste länger werden, obwohl in der synchron laufenden stationären Uhr exakt ein Anschlag erfolgt (3).
Wie geht das zusammen? Also noch einmal: Die stationäre Uhr macht einmal „tick/tack“ und die gleitende Lichtuhr auch – zeitgleich, versteht sich. Der Weg, den das Photon in der stationären Uhr zurücklegt, entspricht dem errechneten Weg in Lichtgeschwindigkeit. Der Weg des Photons in der gleitenden Lichtuhr ist wie wir gerade sahen, länger, die Geschwindigkeit des Photons bleibt jedoch gleich. Das Zeitintervall von „tick“ nach „tack“ ist aber für beide Uhren ebenfalls gleich, was ein Beobachter bestätigen würde. Um diesem Dilemma zu entgehen, postuliert die spezielle Relativitätstheorie, dass die Zeit in dem gleichen Zeitraum von „tick“ nach „tack“ in der gleitenden Lichtuhr langsamer gelaufen sein muss als in der stationären. Es wird also neben der gemessenen Zeit von „tick“ nach „tack“ noch eine „Geschwindigkeit“ des Zeitverlaufs eingeführt. Das ist zweifellos revolutionär, erhält die Zeit doch damit quasi eine stoffliche Eigenschaft – eine Fließgeschwindigkeit.
Man könnte die gleitende Lichtuhr aber auch unter dem Aspekt zusammengesetzter Bewegungen betrachten. Bei der „Verlängerung“ des Weges, den das Photon in den Augen eines äußeren Beobachters zu bewältigen hat, treten nämlich zwei Bewegungen in Erscheinung. Erstens, die Bewegung der Uhr und zweitens die Bewegung des Photons. Beginnen wir mit der Bewegung der Uhr. Unser Beobachter befindet sich mit der Uhr in einem Bezugssystem, in ein und demselben definierten Raum. Nehmen wir unsere Überlegungen zu dem gleichmäßig dahinfahrenden Zug zur Hilfe, dann ist die gleitende Lichtuhr gewissermaßen der Zug. Ein Beobachter am Bahndamm sieht die Bewegung des Zuges in der Landschaft, die er auch messen kann. Wenn die Rollos geschlossen sind, kann er nicht sehen, was im Zug passiert. Bewegungen im Zug kann er nicht messen. Einem Beobachter der Lichtuhr kann Ähnliches geschehen, zum Beispiel dann, wenn sich die Lichtuhr in einem geschlossenen Kasten befindet. Dann kann er die Bewegung der Photonen weder sehen noch messen. Nur die Bewegung der Lichtuhr ist vom Standpunkt unseres Beobachters eine relative Bewegung, die er messen kann. Sie befindet sich mit ihm in einem Bezugssystem.
Soweit zur Lichtuhr. Dann ist da noch die Bewegung des Photons. Hinsichtlich der Bewegung des Photons innerhalb der Lichtuhr ist der Beobachter ein außerhalb stehender Dritter, der nicht zum Bezugssystem gehört. Wenn sich die Lichtuhr in einem geschlossenen Kasten befände, dann kann er nicht einmal wahrnehmen, ob es in der Lichtuhr überhaupt eine Bewegung gibt. Falls er jedoch in die Lichtuhr hineinschauen kann und dort eine Bewegung registriert, dann muss er sich im Klaren sein, dass die Bewegung innerhalb der Lichtuhr von außen nicht zweifelsfrei messbar ist. Messen könnte er nur, wenn er sich selbst in relativer Ruhe zu diesem Bezugssystem befände. Dazu müsste er sich parallel zur Lichtuhr und mit der gleichen Geschwindigkeit wie diese bewegen. In diesem Fall würde er allerdings zu dem gleichen Messergebnis gelangen wie bei einer stationären Uhr. Wenn sich nun der Beobachter nicht vom Fleck rührt und trotzdem die Bewegung innerhalb der gleitenden Lichtuhr untersuchen will, so muss er wieder die beiden Bewegungen – Bewegung der Uhr und Bewegung des Photons – unterscheiden. Die angenommene Diagonalbewegung als Resultante beider Bewegungen ist, genau besehen, eine Sinnestäuschung, denn es werden zwei Bewegungen unterschiedlicher Bezugsebenen vermischt. Im übrigen, ein Männlein auf dem Mars, das unser Experiment mit Interesse verfolgt, hätte neben der Bewegung des Photons und der Bewegung der Lichtuhr auch noch die relative Bewegung der Erde im Verhältnis zum Mars bei der Bewertung seiner Beobachtungen zu berücksichtigen.
Die spezielle Relativitätstheorie macht hinsichtlich der verschiedenen Bezugssysteme für Messungen keine Unterschiede. Ganz egal, von wo aus man die Geschwindigkeit des Lichts ermittelt – ob vom Mars, ob als stationärer Beobachter einer gleitenden Lichtuhr oder als sich parallel zur Lichtuhr bewegend – sie muss immer gleich groß, eben Lichtgeschwindigkeit sein. Blicken wir an dieser Stelle noch einmal zurück auf unsere Überlegungen im Zusammenhang mit der Verbrecherjagd und der dazugehörenden Schießerei. Die Kugel erhält ihre Geschwindigkeit durch den Impuls, der von der Waffe ausgeht. Die Aufprallenergie in Bezug auf das parallel fahrende Auto wird genau von diesem Impuls bestimmt. Beim Aufprall der Kugel auf einen Baum am Straßenrand kommt jedoch zur Energie der Kugel die Energie aus der Annäherung des Autos an den Baum hinzu. Das heißt beim Aufprall addieren sich beide Energiemengen, ohne dass sich die Geschwindigkeiten der Kugel oder des Autos veränderten.
Auf die Lichtuhr bezogen heißt das, würde das Photon aus der gleitenden Lichtuhr auf ein Hindernis treffen und seine Energie abgeben, dann wäre die durch das Hindernis zu absorbierende Energie gleich der Summe aus der Energie des Photons plus der Energie die der Bewegung der Lichtuhr entspricht. Wenn man eine zusammengesetzte Bewegung in Bezug auf das Licht allerdings verneint, dann würde dies bedeuten, dass beim Zusammenstoß des Photons mit einem Hindernis, nur die Energie des Photons abgegeben wird, weil die Energie aus der Bewegung der Lichtuhr im Dogma der speziellen Relativitätstheorie „verschwunden“ ist. Diese Überlegung soll mit einem zugespitzten Beispiel weiter verdeutlicht werden. Man nehme zwei Photonen, die sich mit Lichtgeschwindigkeit bewegen, jedoch in entgegengesetzter Richtung. Obwohl sich nun beide Photonen mit Lichtgeschwindigkeit bewegen, entfernen sie sich nicht etwa mit doppelter Lichtgeschwindigkeit voneinander, sondern – so die Spezielle Relativitätstheorie – mit einfacher Lichtgeschwindigkeit. Verwundert reibt man sich die Augen. Ein Photon verkörpert ein bestimmtes Quantum an Energie, das sich in seiner Freuquenz und seiner Ausbreitung in Lichtgeschwindigkeit ausdrückt. Die Frequenz der betrachteten Photonen sei gleich und soll in unserer Betrachtung außen vor bleiben. Nennen wir den verbleibenden Teil des Quantums, der sich in der Ausbreitung mit Lichtgeschwindigkeit ausdrückt, Energie A. Zwei gleichartige Photonen verkörpern demnach Energie in einer Größe von 2 x A. Bestimmt man nun die Energie, mit der sich die Photonen voneinander entfernen, dann wird aus der Größe 2A mit einem Mal 1A, da sie sich ja nur mit einfacher Lichtgeschwindigkeit voneinander entfernen sollen. Das andere Quantum A ist verschwunden. Aber keine Sorge, betrachten wir die Bewegung der Photonen nicht mehr in Bezug aufeinander, sondern in Bezug auf andere Objekte, dann taucht die Energie, wie aus dem Nichts, wieder auf. Das heißt, Energie entsteht oder verschwindet, je nach dem wie wir sie messen. Aha!?
Einstein hatte die Existenz einer absoluten Geschwindigkeit des Lichts zusammen mit dem Äther verworfen und postuliert, nur relative Bewegungen des Lichts seien physikalisch relevant, da nur diese gemessen werden können. Richtig ist, dass nur relative Bewegungen des Lichts messbar sind, was nichts anderes heißt, als dass man für das Messen einer Bewegung einen Bezugspunkt, ein Bezugssystem braucht. Das gilt allerdings für jegliches Messen, denn das Messen ist immer ein Vergleichen verschiedener Objekte oder Sachverhalte mit einem Maßstab. Der Maßstab ist das Bezugssystem, im Verhältnis zu welchem die relative Bestimmung von Eigenschaften erfolgt. Die Existenz dieser Eigenschaften hängt jedoch nicht vom Bezugssystem ab oder davon, dass man sie messen kann. Man hat, zum Beispiel, den absoluten Nullpunkt nie gemessen, trotzdem wird niemand seine Existenz als Grenzwert bestreiten. Ähnliches gilt im übrigen auch für die Lichtgeschwindigkeit. Als Lichtgeschwindigkeit bezeichnet man die Ausbreitungsgeschwindigkeit der Photonen im leeren Raum. Sie stellt ebenfalls einen Grenzwert dar, da es kein Objekt gibt, dass eine höhere Geschwindgkeit erreichen kann. Deshalb ist es nicht möglich, die Geschwindigkeit des Lichts direkt zu messen, denn dafür müsste es ein Messinstrument geben, das sich schneller als das Licht bewegt. Es sind jedoch indirekte Messungen möglich, mit deren Hilfe man diesen Grenzwert recht genau emitteln konnte. Der Fakt, dass die absolute Geschwindigkeit des Lichts nicht direkt gemessen werden kann, ändert jedoch nichts daran, dass sie eine reale Größe ist, wie theoretisch und praktisch immer wieder bestätigt wurde. Selbst Einsteins Theorien basieren auf dem Wert der „eigentlich“ nicht messbaren absoluten Geschwindigkeit des Lichts.
Quellen:
- Stephen W. Hawking: Eine kurze Geschichte der Zeit. Die Suche nach der Urkraft des Universums; Lizenzausgabe mit Genehmigung des Rowoldt Verlags, Reinbek, Copyright 1988
- Julian Schwinger: Einsteins Erbe. Die Einheit von Raum und Zeit; 2. Auflage 1988, Spektrum der Wissenschaft, Heidelberg
- Brian Greene: Das elegante Universum. Superstrings, verborgene Dimensionen und die Suche nach der Weltformel; Siedler Verlag 2000, Copyright des Originals 1999
(1) vgl. B.Greene S. 50 und J.Schwinger S. 21
(2) vgl. B.Greene S.55 ff und J. Schwinger S. 46 ff
(3) vgl. B. Greene S.56/57
(4) vgl. B.Greene S.65 ff
Bild: imagesCA873JA5
zuletzt geändert: 06.06.2019